Random บน Computer สุ่มแบบไหนเราถึงเรียกว่าสุ่ม ?
/ 8 min read
เรื่องมันเริ่มจากสุ่มของ
เคยสงสัยกันไหมครับ เวลาที่เราทอยลูกเต๋า สุ่มหยิบการ์ดออกจากกอง หรือแม้แต่สุ่มโดยการทอยเหรียญ สิ่งนี้เมื่อย้ายเข้าไปทำงานอยู่บนคอมพิวเตอร์มันทำงานยังไง เรื่องนี้มันเกิดขึ้นตอนที่ผมพยายามจำลองการสร้าง software ของเกมๆหนึ่ง แล้วก็มาติดใจกับคำสั่ง Math.random() (ในภาษา javascript) ที่ตัวเองกำลังจะใช้ว่า เอ๊ะ แล้วการสุ่มในคอมพิวเตอร์มันทำงานยังไง ทั้งๆที่แม้แต่ตัวเราเองยังไม่สามารถอธิบายการสุ่มได้เลยว่ามันทำงานยังไง แล้วไอ Math.random() นี่มันจำลองการสุ่มแบบไหนออกมากัน มันมั่นใจได้ยังไงว่ามันสุ่มอยู่จริงๆ ก็เลยเป็นที่มาของบทความนี้แหละครับ
มนุษย์เราสุ่มของยังไง
สมมุติ ว่า เราลองให้ผู้อ่านนึกถึงตัวเลขใดก็ได้ 1–10 ไว้ในใจ (พูดเลขออกมาด้วยได้นะ) ทุกคนจะเจอว่า เราจะไม่สามารถอธิบายเป็นเหตุผลได้ว่า ทำไมเราถึงเลือกเลขนั้น นอกจากความรู้สึกที่มีต่อเลขนั้นแค่นั้น เช่น ช่วงนี้โชคดีกับเลขนี้, ไม่รู้สิ แค่หยิบมาเฉยๆ, ชอบ 7 เยอะๆ ก็เลยเลือก 7
ตั้งแต่ในอดีต ไม่ว่าจะเป็นการสุ่มของรับรางวัล, การสุ่มเพื่อตัดสินใจ, การสุ่มเพื่อทำนายอนาคต หรือแม้แต่การเล่นเกม เราก็ล้วนใช้ของที่จับต้องได้เป็นสื่อกลางในการสุ่มค่าออกมาหมด เพื่อให้เกิดการตัวเลขสุ่มที่ได้ออกมาเป็นไปอย่างยุติธรรมที่สุด เช่น ลูกเต๋า (ทอย 1–6), เหรียญ (คว่ำ / หงาย), หยิบเลขบอลจากกล่อง , ล้อหมุน (เอาจริง ทุกวิธีที่เล่ามาก็ยังใช้งานกันมาจนถึงปัจจุบันนี้นะ)
แต่ทีนี้เมื่อโลกเข้าสู่ยุคของการรุ่งเรืองทางวิทยาศาสตร์ ช่วงราวๆ ศตวรรษที่ 19 ซึ่งในสมัยนั้น เหล่านักวิจัยเริ่มสนใจในเรื่องการใช้ตัวเลขสุ่มมากขึ้นในงานที่เกี่ยวข้องกับวิทยาศาสตร์ และ คณิตศาสตร์มากขึ้น เนื่องจากเป็นยุคสมัยที่ผู้คนเริ่มทำการทดลอง ตัวเลขสุ่มมันก็เลยมีประโยชน์ในฐานะ “เพิ่มเงื่อนไขพิเศษที่เราควบคุมไม่ได้” เข้าไป เช่น
- ใช้ตัวเลขสุ่มในการกระจายการหยิบกลุ่มคนมาทดลองแบบสุ่ม จะหยิบจากเมืองไหน จะหยิบมากี่คน คนนั้นควรจะเจอแบบทดสอบแบบไหน (คล้ายๆ A/B Testing ในปัจจุบัน)
- การใช้ตัวเลขสุ่มสามารถใช้ในการจำลองสถานการณ์ทางธรรมชาติต่างๆที่เราควบคุมไม่ได้ เช่น การจำลองการแพร่ระบาดของโรค การจำลองภาวะอากาศ หรือการจำลองพฤติกรรมของระบบทางธรรมชาติ ซึ่งช่วยให้นักวิทยาศาสตร์และนักคณิตศาสตร์สามารถทดสอบและพัฒนาทฤษฎีและโมเดลต่างๆ ได้
- ในการวิเคราะห์ข้อมูลสถิติหรือข้อมูลที่เป็นผลลัพธ์จากการสำรวจหรือการทดลองต่างๆ การใช้ตัวเลขสุ่มช่วยให้สามารถสร้างความหลากหลายในข้อมูลและทดสอบสมมติฐานได้
ซึ่งแน่นอนเมื่อเราพูดถึงช่วงเวลานั้น เรายังไม่ได้มีเครื่องสุ่มอะไรอย่างเป็นรูปธรรมออกมา วิธีการสุ่มมันก็เลยจะหลากหลายมาก เช่น ทอยลูกเต๋า, ใช้เลขทะเบียนตามร้านค้า (หรือเลขอะไรก็ตามที่เห็นก็หยิบเลขนั้นมาใช้เลย), ใช้ตัวเลขทางธรรมชาติ (เช่น ใช้เวลาการตกของฝนของวันนั้น) หรือการสร้างคำถามเพื่อให้อีกคนตอบเป็นตัวเลขสุ่มออกมา เป็นต้น ซึ่งมันก็ดูจะไม่ใช่หนทางที่ดีสำหรับนักวิจัยเท่าไหร่ (นึกภาพตัวเองที่วันๆจะต้องมาพยายามสุ่มเลข เอาจริงก็เปลืองสมองใช่เล่นเหมือนกันนะ)
ในช่วงปี 1940 จึงได้มีคนกลุ่มหนึ่งชื่อ RAND Corporation ได้สร้างหนังสือชื่อ A Million Random Digits with 100,000 Normal Deviates หนังสือเล่มนี้ไอเดียเขาคือ เราจะทำการสุ่มตัวเลขจำนวนมากมาไว้ในหนังสือเล่มนี้ ทั้งตัวเลขที่ใช้งานได้เป็นแบบตัวเลขทั่วไปเรียงกันเป็น sequence (sequence คือเรียงตัวเลขต่อกันไปเรื่อยๆ ตามภาพตัวอย่างด้านล่าง) และตัวเลข standard normal deviate (ตัวเลขค่าเบี่ยงเบนมาตรฐานที่ออกจากค่าเฉลี่ย — ที่ใช้ในสถิติ) ซึ่งตัวเลขในหนังสือก็มีจำนวนมากจริงๆนะ เพราะหนังสือมันไม่มีอะไรเลยนอกจากตัวเลขสุ่มในหนังสือประมาณ 600 หน้านี้ เบื้องหลังของตัวเลขเหล่านี้ คือการใช้ ล้อหมุน (roulette wheel) ต่อเข้ากับคอมพิวเตอร์ (ในสมัยช่วงศตวรรษที่ นั้นคอมพิวเตอร์ ผู้คนยังรู้จักในฐานะวงจรช่วยคำนวนทางคณิตศาสตร์อยู่ จะไม่เหมือนคอมพิวเตอร์ที่เรารู้จักกันในทุกวันนี้นะ) และให้สัญญาณไฟฟ้าเป็นคนหมุนแบบสุ่มที่ล้อหมุนนั้นแทน โดยตัวสัญญาณที่ส่งออกมานั้นจะเป็นการส่งสัญญาณแบบไม่มีลำดับเวลาแน่นอนและไม่สามารถทำนายล่วงหน้าได้ เรียกอีกชื่อหนึ่งว่า Random pulse generator (เรียกง่ายๆว่าสัญญาณที่เกิดขึ้นแบบสุ่ม ซึ่งอาจจะเกิดจากการผสมสัญญาณหลายๆแบบที่เราเรียกกันว่า noise ผสมเข้าไปจนไม่สามารถคาดเดาได้) อันนี้เป็นวิธีการโดยประมาณนี้ที่หนังสือเล่มนี้ใช้นะ เนื่องจากหนังสือเองก็ไม่ได้เผยแพร่โดยละเอียดเช่นกันว่าตัวเองสุ่มตัวเลขออกมายังไงได้เยอะแยะขนาดนี้
ตัวอย่างหนังสือ “A Million Random Digits with 100,000 Normal Deviates”
 (ดูตัวอย่างเต็มหรือใครสนใจจะสั่งซื้อไปตามได้ที่ https://www.amazon.com/Million-Random-Digits-Normal-Deviates/dp/0833030477)
(ดูตัวอย่างเต็มหรือใครสนใจจะสั่งซื้อไปตามได้ที่ https://www.amazon.com/Million-Random-Digits-Normal-Deviates/dp/0833030477)
ถ้ามองภาพให้ง่ายขึ้น ไอเดียของสิ่งนี้ มันคือ
การสุ่ม จาก ค่าของสัญญาณไฟฟ้าแบบไม่สามารถทำนายล่วงหน้าได้ออกมาเป็นตัวเลข
และนี่ก็นำมาสู่ไอเดียยุคแรกๆของการสุ่มที่คอมพิวเตอร์ที่ยังไม่ได้สลับซับซ้อนมากนัก ไอเดียนี้ก็ถูกนำมาประยุกต์ใช้กับหลายๆเคสในยุคนั้น
อย่าง E.R.N.I.E. ระบบสร้างตัวเลขสุ่มที่ใช้ในการจับรางวัลในการลุ้นหวย Premium Bond ใน UK ไอเดียโดยประมาณจะคล้ายๆกันคือ ใช้อุปกรณ์วัดค่าเสียงและประมวลผลเสียงรบกวนที่เกิดขึ้นเพื่อสร้างตัวเลขสุ่มที่ไม่สามารถทำนายล่วงหน้าได้ (อันนี้เล่าแบบง่ายๆนะ แต่วิธีการที่ทำให้ได้สัญญาณแบบสุ่มมามันหลายขั้นตอนกว่านั้นเยอะ ใครสนใจ ตามอ่านใน link ใต้ภาพได้)

ภาพจาก https://ernie.virtualcolossus.co.uk/ernie.html
หรืออย่างปี 1951 คอมพิวเตอร์อย่าง the Ferranti Mark 1 (ที่ Alan Turing มีส่วนเกี่ยวข้อง) เองก็มีเครื่องที่ทำการสร้างคำสั่งสุ่มส่งมาพร้อมกับเครื่องคอมพิวเตอร์เลย คำสั่งสุ่มนั้นสามารถสุ่มตัวเลขได้ 20 bit ในครั้งเดียวโดยใช้สัญญาณรบกวนของไฟฟ้า (noise)
นี่คือภาพเครื่อง Ferranti mark 1
ซึ่งทั้งหมดนี้ ยังคงอยู่บนพื้นฐานเดียวกันคือ
การสุ่ม จาก ค่าของสัญญาณไฟฟ้าแบบไม่สามารถทำนายล่วงหน้าได้ออกมาเป็นตัวเลข
มั่นใจได้ยังไงว่านี่คือการสุ่ม ?
ก่อนจะไปต่อเรื่องทำให้คอมพิวเตอร์ที่เรารู้จักในปัจจุบันสุ่มได้ ตั้งคำถามกันก่อนว่า ทำยังไงเราถึงจะมั่นใจได้ว่านี่คือการสุ่ม ?
นี่คือคำถามที่สำคัญที่เราควรจะต้องตั้งคำถามก่อนที่เราจะไปยังหัวข้อต่อไปคือ
การสุ่ม คือ อะไร ?
จากเนื้อหาข้างบนที่เราพูดถึงตั้งแต่การสุ่มในอดีต → A Million Random Digits → E.R.N.I.E → Ferranti Mark 1 สิ่งที่เราพอจะสรุปจากเหตุการณ์เหล่านี้ได้คือ
การสุ่ม คือ การเกิดขึ้นของบางสิ่งแบบไม่มี Pattern
เช่น การทอยเต๋า, การโยนเหรียญ, การหยิบตัวเลขออกจากกล่อง (ดังเช่น วิธีการมาของตัวเลขหวยของประเทศเรา) หรือการหยิบ noise ของสัญญาณไฟฟ้ามา เราไม่สามารถบอก Pattern มันได้เลยว่า ทำไมต้องเป็นเลขนี้ ออกมา เราจึงสามารถเรียกสิ่งนี้ได้ว่าเป็น “การสุ่มโดยแท้จริง”
ดูเผินๆก็เหมือนโลกเราจะค้นพบการสุ่มเรียบร้อยแล้วตั้งแต่ช่วงกลางศตวรรษที่ 19 เรามีเครื่องที่สามารถสุ่มได้จากสัญญาณไฟฟ้า และเราก็ได้ตัวเลขสุ่มออกมาแล้วและสามารถตอบโจทย์การสุ่มได้แล้ว เราจะเขยิบตัวเองกันอีกนิดไปในยุคที่เริ่มมีการพูดถึง Program (หรือ Software) กัน
จุดเริ่มต้นของการสุ่มแบบ Pseudorandom number generator
ทีนี้ถ้าเราลองย้อนกลับไปดูเครื่องสุ่มอย่างตอน A Million Random จนถึง Ferranti Mark 1 เราจะค้นพบอีกหนึ่งอย่างเช่นกันว่า “ทำไมการสุ่มมันสร้างขึ้นมายากเช่นนี้” มันไม่ใช่เพียงแค่การสร้างของชิ้นหนึ่งแล้วสุ่มได้เลย แต่มันคือการสร้างวงจรบางอย่างขึ้นมาเพื่อให้สุ่มได้ มันเลยจะส่งผลทำให้เราเจอกับความไม่แน่นอนสูง เนื่องจากมันคาดเดาไม่ได้เลยว่าจะเกิดอะไรขึ้นในวงจรระหว่างการสุ่มบ้าง เมื่อเข้าสู่ยุคสมัยที่คอมพิวเตอร์เริ่มสามารถเขียน “Program” ใส่ลงไปได้ (แถวๆยุคของ ENIAC, The Manchester Mark 1) มันเลยนำไปสู่ปัญหาของ การสุ่มบน program บนระบบคอมพิวเตอร์ในเวลาต่อมา
เพื่อให้เรื่องนี้นึกภาพออกได้ง่ายขึ้น เราลองนึกภาพเราทำ “Program” สักตัวหนึ่ง และใน program นั้นมีจุดที่ต้องสุ่มเลขออกมาใช้ (ต้องย้อนกลับไปสมัยนั้นด้วยนะ) แล้วใช้การสุ่มเลขแบบวิธีด้านบนที่เราเล่ามา การสุ่มเลขจะกลายเป็นต้องมาขึ้นอยู่กับแผงวงจรการสุ่ม สิ่งที่จะเกิดขึ้นคือ เราอาจจะต้องมาเสี่ยงด้วยว่า วงจรการสุ่มนั้นมันจะทำงานได้ปกติดีหรือไม่ ? วงจรมันไม่ได้พังใช่ไหม ? มันจะสุ่มออกมาแล้วเป็นเลขสุ่มจริงๆใช่ไหม ? เพราะคนทำ program ก็อาจจะไม่ได้รู้เหมือนกันว่ามันสุ่มออกมาแบบไหนจากวงจร มันทำให้การสุ่มนั้นเกิดความ “ไม่แน่นอนในการดึงเลขสุ่ม” (uncertainty) ออกมา ซึ่งจริงๆ program มันควรจะอยู่บนพื้นฐานของความ “แน่นอน” และ “สามารถทำซ้ำได้” (consistently) เพื่อให้ตัว program เองสามารถทดสอบผลลัพธ์ที่แท้จริงของตัว program ได้เช่นเดียวกัน
เพราะฉะนั้นการสุ่มของ Computer ในยุคต่อมาบน Program (Software computer) คือ
การสุ่มคือ สิ่งที่ต้องสามารถทำซ้ำได้ และให้ผลลัพธ์ที่แน่นอนออกมา
หรือ ถ้าตีความเป็นภาษาคอมพิวเตอร์ขึ้นคือ
การสุ่มคือ deterministic function (function ที่ต้องให้ผลลัพธ์ออกมาเหมือนเดิมเสมอ เมื่อ input ยังเหมือนเดิม) ที่สุ่มได้
มันเลยนำมาสู่ไอเดียที่ว่าด้วยเรื่องของการสุ่ม แบบ Pseudorandom number generator (เรียกย่อๆว่า PRNG แต่ในบทความนี้จะขอเรียกว่า Pseudorandom แทนเพื่อให้จำได้ง่ายขึ้น) หลักการสร้าง random number sequence ด้วย deterministic function คือใช้ function เดียวกันวนซ้ำในการสร้าง random number sequence ออกมา
ช่วงปี 1946 John von Neumann ได้คิดค้นไอเดียในการทำ Psuedorandom ขึ้นมาชื่อ middle-square method concept ถ้าเล่าเป็น code ก็จะตามด้านล่างนี้ (เดี๋ยวผมมีอธิบายตัวอย่างเพิ่มไปนะ ถ้าใครไม่สันทัดเป็น code ก็ข้ามไปได้)
# Code นี้หยิบมาจาก wiki ของ middle-square method concept
# เลือก seed number เริ่มต้นมา 1 ตัว (ตัวเริ่มต้นการสุ่ม) สำหรับ code นี้จะเป็นการสร้าง random sequece สุ่มเลข 4 digitseed_number = int(input("Please enter a four-digit number:\n[####] "))number = seed_number
# สร้าง set ชื่อ already_seen สำหรับเก็บ random number sequencealready_seen = set()counter = 0
# วน loop ไปจนกว่าจะกลับมาเจอเลขซ้ำwhile number not in already_seen: counter += 1 already_seen.add(number) # นำเลขที่สุ่มได้มาใส่ set already_seen number = int(str(number * number).zfill(8)[2:6]) # จาก code ด้านบนคือ นำตัวเลขนั้นมา ยกกำลัง 2 (เช่น 1112^2 = 1236544) # และ เพิ่มเลข 0 นำหน้าเลขนั้นให้ครบ 8 digit (1236544 > 01236544) # และ ดึงแค่เฉพาะ 4 digit ที่อยู่ตรงกลาง 01236544 > 01"2365"44 ออกมา ใช้เป็นเลข number ต่อไป print(f"#{counter}: {number}")
# ผลลัพธ์ตรงนี้เราก็จะได้ว่า# already_seen ก็คือ set เลขสุ่มที่เจอทั้งหมดในรอบนี้# counter คือ กี่ตัวเลขกว่าจะวนกลับมาเจอเลขเดิมอีกรอบ (เพราะเลขเดิมจะส่งผลทำให้ค่าหลังจากนี้มันเหมือนเดิม)print(f"We began with {seed_number} and" f" have repeated ourselves after {counter} steps" f" with {number}.")อธิบายเป็นตัวอย่าง ให้เห็นภาพมากขึ้น
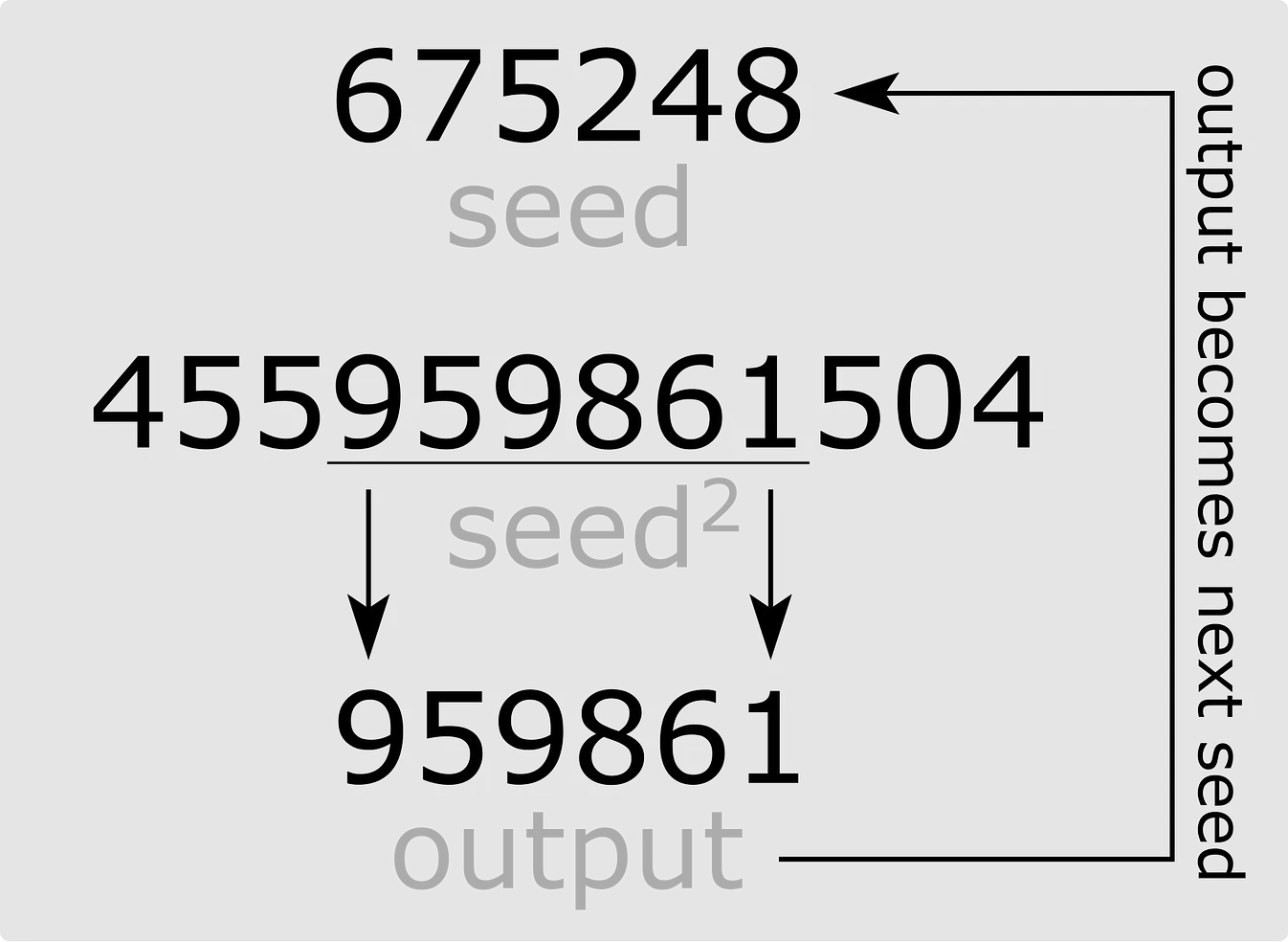
- ตามภาพที่อยู่ด้านล่าง ภาพแรกคือตัวอย่างของการ run algorithm นี้โดยเป็นการสุ่มเลข 6 digit สมมุติเรากำหนด seed เป็น 675248 (จำนวนหลักที่เราจะสุ่มจะเป็นไปตาม digit ของเลข seed ที่เรากำหนด) เราจะนำเลขนั้นมายกกำลังสอง เป็น 455959861504 หลังจากนั้น เราก็จะหยิบตรงกลาง 6 digit ของเลขนั้น 455”959861”504 = 959861 ออกมา เลขนี้ก็จะกลายเป็นเลขที่เราจะใช้ทำในรอบต่อไป
- เราจะทำแบบนี้ซ้ำไปเรื่อยๆจนกว่า sequence จนวนกลับมาเจอเลขซ้ำ (แปลว่า การสุ่มนั้นได้วนกลับมาที่เดิมแล้ว) เราก็จะได้ sequence ของตัวเลขสุ่มออกมาชุดหนึ่งที่เราสามารถหยิบไปใช้ได้ (เช่นตัวอย่างนี้ก็จะเป็น 959681, 987621, 395239, …)
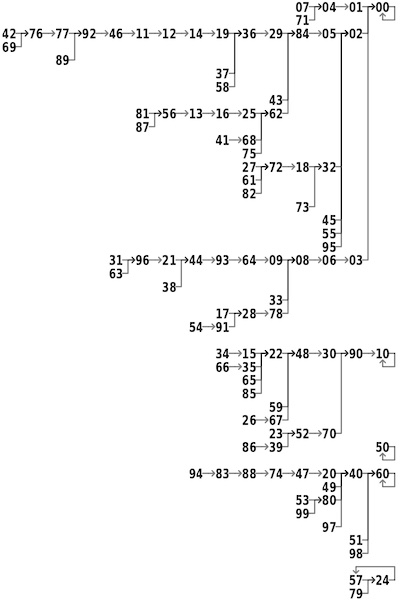
- ภาพที่สอง เป็นตัวอย่างของการสุ่มของตัวเลข 2 digit ไปเรื่อยๆจนท้ายที่สุดก็จะเจอจุดกลับมาซ้ำกัน
และนี่คือตัวอย่างภาพที่วนกลับมาซ้ำ
เชื่อว่าหลายคนที่อ่านมาถึงจุดนี้ ต้องกำลังคิดเหมือนกันว่า “นี่มันไม่ใช่การสุ่มแล้วนี่นา” ถูกต้องครับ computer เรา ถ้าลำพังอาศัยสิ่งที่เรียกว่า Program หรือพลังของ Software เพียงอย่างเดียว เอาจริงแล้วไม่ได้ถือว่าเป็น “การสุ่มที่แท้จริง” ตามที่เราเคยพูดถึงเรื่องการสุ่มที่เคยกำหนดไว้ เพราะวิธีการนี้มันมีสิ่งที่เรียกว่า “Pattern” ซ่อนอยู่ แต่เพื่อยังคงหลักการว่า อยากให้ Program เป็นสิ่งที่มีความ “แน่นอน” และ “สามารถทำซ้ำได้” Program จึงควรเป็นสิ่งที่ deterministic อยู่ นี่จึงเป็นไอเดียที่ถือว่า “ดีเพียงพอ” สำหรับการสุ่มของคอมพิวเตอร์ ขอเพียงแค่มี pattern ที่ “ยาวมากพอ” ก็จะสามารถทำให้สิ่งนี้ใกล้เคียงกับการสุ่มที่แท้จริงได้

(ภาพ: Deterministic function คือ function ที่ใส่ input อะไรเข้าไป output ต้องออกมาเหมือนเดิม)
ในช่วงนั้น เมื่อการสุ่ม Pseudorandom เริ่มเป็นที่ถูกพูดถึงกัน นักคณิตศาสาตร์จำนวนหนึ่ง จึงพยายาม improve Pseudorandom จาก 2 อย่างเพื่อให้ใกล้เคียงกับความสุ่มทางธรรมชาติมากขึ้นคือ
- ทำยังไงให้ Seed (ค่าเริ่มต้น) เป็นสิ่งที่คาดเดาได้ยากที่สุด
- ทำยังไงให้ Random number sequence มี Pattern ยาวที่สุดเท่าที่จะเป็นไปได้
ทั้ง 2 อย่างนี้ถือเป็นหัวใจสำคัญของ Pseudorandom เลยนะ อย่างน้อยที่สุดแม้ว่านี่จะเป็นการสุ่มที่มี Pattern แต่เป็น Pattern ที่เดาได้ยากจัดๆ (เกินกว่าปัญญาของมนุษย์และคอมพิวเตอร์จะหา Pattern เจอได้) ซึ่งแน่นอนอย่างไอเดียของ middle square method ก็มีจุดอ่อนคือ Pattern ที่ค่อนข้างสั้น เพราะฉะนั้น ถ้าเราเอาวิธีนี้ไปใช้งานจริง ด้วยความสามารถของคอมพิวเตอร์ใช้เวลาไม่นานมากก็จะสามารถหา Pattern วนกลับมาได้แล้ว (โดยเฉพาะกับตัวเลขน้อยๆ)
ในปี 1949 มีไอเดียใหม่ชื่อ Linear congruential generator

หลักการคือ เราจะกำหนดค่าเริ่มต้นคือ seed (X₀) ใส่ deterministic function ที่มี a เป็นตัวคูณ, c เป็นตัวเพิ่ม และ m เป็นตัว modulus (อธิบายเพิ่ม modulus แทนด้วยสัญลักษณ์ % ในคอมพิวเตอร์ คือเอาเศษหลังการหารด้วยตัวเลขนั้นออกมา เช่น 7 % 3 จะได้ค่า 1 ออกมาเนื่องจาก 7 หารด้วย 3 จะเหลือเศษ 1 ออกมา เท่ากับว่าตัวเลขสูงสุดของการ modulus ที่เกิดขึ้นได้คือเท่ากับตัวหารนั่นเอง ทั้งนี้ใน function นี้ทำเพื่อกันไม่ให้มีตัวเลขมากเกินขอบเขตเลขสูงสุดที่ใช้เก็บของ random sequence นี้) แล้วเราก็จะ run สิ่งนี้ไปเรื่อยจนได้ random number sequence มา
นี่คือตัวอย่าง Linear contruential generator เป็นฉบับภาพ

คำถามคือ เมื่อไหร่เลขจะวนกลับมา เป็น pattern เดิมซ้ำ คำตอบก็คือ ขึ้นอยู่กับตัวแปรที่ใช้ โดยเฉพาะตัว m ยิ่งถ้าเป็น m เป็น prime number ที่เยอะมาก period ของ pattern ก็จะอยู่ที่ m-1, ถ้า m เป็น เลขสองยกกำลัง (ex. 2⁴) period ก็จะอยู่ที่ 2³² หรือ 2⁶⁴ เท่ากับว่า แม้จะเป็น pattern ที่วนกลับมาได้เหมือนเดิม แต่กว่าจะกลับมาเจอได้ โดย practical จริงๆ คือมันจะนานมากกว่าจะสามารถหาเจอได้ (แต่ในปัจจุบัน เรามี algorithm ที่มีประสิทธิภาพมากกว่านี้และนะ แต่ไอเดียนี้ถือเป็นรากฐานของไอเดียการสุ่ม Pseudorandom ที่ใช้มาจนถึงปัจจุบันนี้ด้วย)
ทีนี้ เราลองกลับมาพิจารณา deterministic function ของ Random แบบ Pseudoramdom อีกที สมมุติว่า
- เรารู้ว่า function ของ Random นั้นคืออะไร
- เราพยายามเดา seed สักค่าหนึ่งออกมา ปรากฎว่า ถูกต้องตามระบบที่ใช้ function นั้น
จะเท่ากับ เราจะสามารถรู้ Pattern ที่แท้จริงของ Random นั้นได้ (ซึ่งเอาจริงๆ มันก็ไม่ได้ง่ายขนาดนั้นนะ) แต่ตามทฤษฎีคือ ถ้าเรามีความพยายามเดา seed ที่มากพอ กับ พยายาม run sequence number ให้จบ sequence (กลับมายังค่าเดิม) ได้จนครบ ตาม seed ที่เลือกได้ = เราสามารถรู้ Pattern ของการสุ่มได้
มันเท่ากับว่ามันอาจจะไม่มี “ความปลอดภัย” พอที่จะใช้กับเรื่องที่สำคัญมากๆได้นั่นเอง ลองนึกภาพว่า ถ้าเกิดเราใช้สุ่มเรื่องสำคัญเช่นหวย แล้วตัวเลขสุ่มดันมี Pattern เราก็คงไม่วางใจการสุ่มนั้นเช่นเดียวกัน
เมื่อการสุ่มไม่ใช่สุ่มจริงๆ แบบนี้ แล้วถ้าเราจะสุ่มจริงๆละ = True random number generator ช่วยคุณได้
ดังนั้นในช่วงต่อมา (ซึ่งก็ยังวนเวียนใกล้ๆเคียงกับช่วงเวลาเดิมของกลางศตวรรษที่ 19) จึงมีความพยายามกันใหม่ในการทำให้ “การสุ่มที่แท้จริง” เกิดขึ้นบนคอมพิวเตอร์ให้ได้ และเมื่อใดก็ตามที่เราพูดถึงการสุ่ม นิยามก็ยังคงเดิม คือ “การเกิดขึ้นของบางสิ่งแบบไม่มี Pattern” เมื่อเราลองพิจารณาตามหลักการนี้ แปลว่าเราต้องทำให้ Random function ที่จะเดิมใน Pseudorandom เรานิยามมันเป็น deterministic function กลายเป็น Non-deterministic function แทน
นิยามของ Non-deterministic function คือ เราใส่ input ค่าเดิม แต่เราได้ผลลัพธ์ที่ไม่เหมือนเดิมออกมา ซึ่งเหตุการณ์นี้จะเกิดขึ้นได้ก็ต่อเมื่อ program มีตัวแปรบางอย่างอยู่ในสภาวะที่ “คาดเดาไม่ได้” อยู่ใน function นั้น (ดังนั้นสิ่งที่จะทำให้เกิดภาวะนี้ขึ้นมาได้จะต้องเป็นสิ่งที่อยู่นอก software ไป ซึ่งก็คือการดึงค่าบางอย่างจาก “โลกของ hardware” มาใช้ร่วมด้วย เพื่อให้ function กลายเป็น Non-deterministic function ขึ้นมาได้ นั่นก็คือที่มาของสิ่งที่เรียกว่า True random number genetor (ย่อๆว่า TRNG แต่ในบทความนี้จะขอเรียกว่า True random แทนเพื่อให้จำได้ง่ายขึ้น) นั่นเอง

(ภาพ diagram ของ True random number generator diagram)
รู้จักกับ Lava Lamp
ในปี 1997 กลุ่มนักวิทยาศาสตร์คอมพิวเตอร์กลุ่มหนึ่งพยายามหาหนทางในการทำ True random นี้ ในไอเดียชื่อว่า LavaRand โดยใช้หลักการที่ว่า ให้เอากล้อง webcam ส่องไปที่กลุ่มของ Lava lamp (โคมไฟที่มีลักษณะคล้ายๆตะเกียง ตามภาพด้านล่างนี้) แล้วนำภาพถ่ายที่ได้จาก webcam (ที่คล้ายๆภาพด้านล่างนี้) ที่เป็น visual data (ข้อมูล pixel บนภาพ) มาแปลงเป็นตัวเลข sequence random number ออกมา (อารมณ์เหมือนแปลง pixel ภาพเป็นตัวเลข แล้วเอาตัวเลขนั้นเข้ากระบวนการแปลงบางอย่างจนเกิดเป็น sequence ของตัวเลขออกมา) เหตุผลที่ผู้คิดค้นเลือกใช้ Lava lamp เพราะเป็นโคมไฟที่มีสภาวะความไม่แน่นอนสูง เนื่องจากอุณหภูมิ, ความเร็วลม หรือแม้แต่ความหนืดของเหลว ก็มีผลต่อแสงไฟที่แสดงออกมาใน Lava lamp ทั้งหมด มันส่งผลทำให้เกิดความแตกต่างของรูปภาพที่ไม่สามารถคำนวนได้ ดังนั้นตัว Lava lamp (และ webcam ที่เป็น hardware สำหรับอ่านค่า) จึงเป็นแหล่งของความไม่แน่นอน (non-deterministic) ในการสุ่มครั้งนี้นั่นเอง
ถ้าใครสนใจรายละเอียดสามารถเข้าไปอ่านสิทธิบัตรเพิ่มเติมได้ https://patents.google.com/patent/US5732138

ถ้าเราลองสรุปหลักการดู นี่คือการทำให้ “Seed (ค่าเริ่มต้น) เป็นสิ่งที่คาดเดาไม่ได้” สิ่งนี้จะเรียกว่า Entrophy source หรือแหล่งข้อมูลของความไม่แน่นอน ของ True random หลักการของ True random คือ “การใช้ Entrophy source มาคำนวนร่วมกันด้วย” ซึ่งถ้าเราลองคิดตาม นี่คือวิธีการที่เหมือนกับการ Random ในยุคของ Turing (เครื่อง the Ferranti Mark 1) หรือ the million random เลยนะ คือการใช้แหล่งที่ “ไม่สามารถคาดเดา” และ “มีความไม่แน่นอน” ได้มาเป็นตัวในการคำนวนค่าสุ่ม แต่เปลี่ยนการสุ่มนั้นให้สามารถนำมาร่วมคำนวนการสุ่มเข้ากับ program ออกมาได้ แค่นั้นเอง
วิธีการหลังจากช่วงนี้เป็นของ True random ก็จะคง concept คล้ายๆกัน เช่น
- RdRand ที่อยู่ในชิพ intel ที่ฝังคำสั่ง Random อยู่ติดกับชิพไปเลย หลักการของมันคือการใช้ ค่า Entropy source จากสิ่งที่ชิพสามารถอ่านค่าได้ เช่น สัญญาณ clock ของชิพ, noise ของ signal (เช่น thermal noise, photoelectrict effect) มาสร้างเป็น Random number ออกมา
- Random.org ที่ดึงค่าสุ่มมาจาก atmospheric noise และใช้ทฤษฎีการกระจายตัวทางสถิติ (Probability distribution) มาแปลงเป็นเลขสุ่มออกมา (เว็บยังเข้าได้จนถึงปัจจุบัน)
นี่คือภาพหลักการในการ design True random number generator

(ภาพจาก https://link.springer.com/article/10.1007/s10773-019-04189-2)
ฟังดูก็เหมือนจะดูดีนะ True random แต่มันก็มีจุดพิจารณาของ True random (ที่ยังคงคล้ายๆเดิม กับตอนที่คิด Pseudorandom) อยู่เหมือนกันคือ
- Speed (ความเร็ว): เนื่องจากทุกอย่างไม่ได้เกิดใน software เพียงอย่างเดียว มันเลยจะมีเรื่องของเวลาในการอ่านค่าด้วยก่อนที่จะเกิดการคำนวน รวมถึงการ process ค่าจาก Entropy source ที่จะทำให้ใช้เวลามากกว่า Pseudorandom
- Resource dependency (การยึดติดกับแหล่งข้อมูลที่อ้างอิงภายนอก): อาจจะเกิดเหตุการณ์ที่ Resource ที่เราใช้ทำ Entrophy source ไม่สามารถอ่านค่าได้ (เช่น sensor ที่ใช้อ่านค่าเสีย) ก็จะเท่ากับ เราไม่สามารถดำเนินการ Random นั้นได้
- Statistical Testing (การทดสอบให้การสุ่มเป็นไปอย่างสุ่มจริงๆ): สิ่งที่สำคัญอีกอันนึงคือ ตัวเลขที่โผล่ออกมาหลังจาก Entropy source จะต้องมีการทดสอบด้วยว่า เป็น “การสุ่มอย่างที่ควรจะเป็นไหม” ลองนึกง่ายๆว่า ถ้าอยู่ๆ Entropy source เกิดอะไรขึ้นไม่รู้ สุ่มได้แต่เลข 1 ออกมาอย่างเดียว เราควรจะต้องทำอย่างไรกับเหตุการณ์นี้ดี เพื่อให้การสุ่มเป็นไปอย่างเหมาะสมมันเลยจำเป็นต้องมีกระบวนการ Post processing เพื่อจัดการทดสอบการสุ่มให้ถูกต้องด้วย เช่น การ check ด้วยวิธี Probability distribution เพื่อวิเคราะห์การกระจายตัวของเลขสุ่ม และกระจายให้ทุกเลขสุ่มเท่าๆกัน เป็นต้น
จาก 3 ข้อที่กล่าวมา อีกสิ่งที่ถือว่าท้าทายที่สุดของการทำ True randomในการ Random number คือ “เราจะมั่นใจได้ยังไงว่า สิ่งที่ส่งออกมาจาก Hardware ที่เป็น Entropy source นั้น Random จริงๆ” ยกตัวอย่างเคสนึงของ RDRand ที่อยู่บนชิพ Intel ที่มีคนตั้ง assumption ไว้ว่า ถ้ามีคนพยายามทำ backdoor ที่จะควบคุมค่าบางอย่างให้ได้ seed ตามที่กำหนดออกมา ก็เท่ากับว่า คนทำ backdoor สามารถควบคุมการ Random ในชิพนั้นได้เลยเช่นกัน
สำหรับผม ความยากของ True random มันคือการ “ทำให้ที่มาของ Seed (Entropy source) ปลอดภัยที่สุด” และ “ต้องทำให้แน่ใจว่าตัวเลขสุ่มนั้นไม่มี Pattern อยู่จริง” จึงจะเรียกได้ว่า การสุ่มนั้น เป็น “การสุ่มที่แท้จริง” ได้
ท้ายที่สุดแล้ว วิธีไหนดีที่สุดในการ Random กันแน่
ถ้าจะตอบคำถามนี้ให้ดีที่สุด เราต้องตั้งคำถามกันก่อนว่า
เราใช้เลขสุ่มทำอะไรบ้างใน computer ?
สำหรับผม ผมจะจำแนกเป็นทั้งหมด 3 อย่างที่เราใช้กันบ่อยๆในโลกของ computer
- Cryptography: ตัวเลขสุ่มเป็นสิ่งที่สำคัญต่อการเข้ารหัสอย่างมาก (และอาจจะมากที่สุดในโลกของ computer เลยก็ได้ว่าได้) เพื่อสร้าง key ที่มีความปลอดภัยขึ้นมา ยิ่งตัวเลขสุ่มยิ่งยากเท่าไหร่ ประสิทธิภาพของอัลกอริทึมการเข้ารหัส (encryption) ก็จะยิ่งมีความปลอดภัยขึ้นได้ จริงๆอันนี้ถือเป็นสิ่งสำคัญมากในทาง computer เพราะความปลอดภัยที่ดีที่สุด คือการที่เราต้องไม่รู้ว่าต้นทางเข้ารหัสมาแบบไหน ซึ่งการใส่ Random number เข้าไปจะช่วยทำให้การเข้ารหัสถูกแก้ไขได้ยากขึ้น ส่งผลต่อความปลอดภัยที่เพิ่มขึ้น
- Statistic: การสุ่มทางสถิติ มีประโยชน์ในการสร้างกลุ่มตัวอย่างแบบสุ่ม, จำลองเหตุการณ์ / ปรากฎการแบบสุ่ม, สร้างตัวแปรแบบสุ่ม หรือการทดสอบแบบสุ่ม ที่ช่วยให้เหล่านักวิจัยสามารถ ทดสอบสมมุติฐานของตัวเองผ่าน computer ได้คล่องตัวขึ้น (เหมือนสมัยอดีตที่มีคนต้องการเลขสุ่มนั่นแหละ)
- Random event: ทอยลูกเต๋า, สับไพ่, การเลือก action ตีของ bot, การ drop item ในเกม หรือ แม้แต่การแสดงผลภาพ banner ต่อเนื่องแบบสุ่ม ทุกอย่างล้วนมาจากการใช้ประโยชน์จากการสุ่มหมดเลย การสุ่มจึงมีประโยชน์ในการสร้างเหตุการณ์แบบสุ่มให้เกิดขึ้นบนคอมพิวเตอร์ได้เช่นกัน
และนี่คือภาพใหญ่ความแตกต่างระหว่าง Psuedorandom และ True random

ทีนี้ เรามาลองพิจารณาเรื่องนี้กันแบบถี่ถ้วนอีกทีระหว่าง Pseudorandom และ True random ในสายตาของคนยุคปัจจุบันกันดีกว่า เพื่อทำการ map กับ case ด้านบน
ฝั่ง Pseudo random number generator
- ปัจจุบัน เรามี algorithm ที่ดีกว่าในอดีตมากมายแล้ว เช่น Mersenne Twister (ที่ใช้ Linear Feedback shift register มาเป็น based concept ต่อยอดอีกที) ซึ่งก็ยังคง concept ความเป็น pattern เหมือนเดิม แต่ต่อให้เป็น pattern ก็ตาม แต่กว่าจะกลับมาซ้ำกันได้อีกคือ 2¹⁹⁹³⁷ — 1 (คือต่อให้รู้ seed ก็ตาม แต่กว่าจะ run หา pattern เจอได้นี่เรียกว่าอาจจะทำให้คอมพิวเตอร์แตกก่อนเลยก็ได้)
- สิ่งสำคัญที่ฝั่งนี้จะ focus กันนอกเหนือจากเรื่องของความยาว Pattern แล้ว อีกสิ่งนึงคือเรื่องของ “ความเร็ว” เนื่องจาก การสุ่มตัวเลขแบบนี้ ถูกสร้างขึ้นมาเพื่อใช้ในการ “สุ่มเลขแบบทั่วไป” ดังนั้น ความเร็วของการสุ่มควรมาจากตัวของวิธีการที่ run software เองมากกว่า
- ด้วยความที่สุ่มเป็น Pattern และมีความเร็วมากกว่า จะเหมาะกับเคสที่เป็น “การสุ่มที่ไม่ซีเรียสเรื่องความปลอดภัย” และ “impact ต่อมนุษย์ไม่สูงมาก” เช่น การสุ่มเพื่อการ จำลองสภาพอากาศ, สุ่มการ drop ของในเกม, สุ่ม content ที่แสดงผลใน banner carousal
ฝั่ง True random number generator
- ปัจจุบัน ยังพัฒนาต่อไปเรื่อยๆ ตั้งแต่การใช้เหตุการณ์ทางธรรมชาติ (Physical Phenomena) มาคำนวนร่วมด้วยเช่น radioactive decay, Hardware-Based Methods (ใช้ค่าจาก CPU) หรือแม้แต่การใช้ Quantum Random Number Generators หรือการใช้ quantum mechanics มาร่วมคำนวนเลขสุ่มด้วย
- ไอเดียของฝั่ง TRNG จุดประสงค์คือการหาเลขสุ่มที่เป็น “สุ่มจริงๆ” มากกว่า การพัฒนาเรื่องความเร็ว เพื่อให้แน่ใจว่า การสุ่มนี้เป็นไป “โดยธรรมชาติอย่างแท้จริง”
- ด้วยความที่สุ่มแบบนี้ที่ยังคงความสามารถ “ไม่สามารถจับ Pattern” ได้ จึงเหมาะสำหรับงานที่เกี่ยวกับ “ความปลอดภัยโดยเฉพาะ” เช่น การ encrypt sensitive data (ข้อมูลส่วนตัว, การเก็บ key ความปลอดภัยในระบบ), งานด้าน Cryptocurrency อย่างการ mining เองก็ใช้การเข้ารหัสแบบนี้เช่นกัน รวมถึงงานประเภทที่ “เหตุการณ์มีผลต่อมูลค่าหรือความเสียหายต่อโลกความเป็นจริง” เช่น การสุ่มเพื่อชิงเงินรางวัลจริงอย่าง Lottery เป็นต้น
ดังนั้น ถ้าจะให้คำตอบกับคำถามนี้ คำตอบก็คือ แล้วแต่เคส แต่ต้องเลือกใช้ให้ถูกต้องตามจุดประสงค์เช่นกัน
ปัจจุบัน Programming language ใช้วิธีการสุ่มแบบไหนกัน
ด้วยความที่การสุ่มทั้ง 2 วิธี มีความสำคัญด้วยกันทั้งคู่ ใน programming เองจึงต้องมีการสุ่มทั้ง 2 แบบ แยก function สำหรับการ random ไว้ด้วยเช่นกัน แต่ไอเดียจะแบ่งออกเป็น Pseudorandom กับ Secure Pseudorandom (Secure PRNG)
จริงๆ Secure Pseudorandom มันควรจะนับเป็น True random นั่นแหละ แต่เนื่องจาก Entropy source ที่ใช้ในการดึง Seed ของ function ส่วนใหญ่ จะขึ้นอยู่กับค่าที่เก็บไว้ใน os (เป็นค่าบางอย่างของ hardware ที่ computer เตรียมไว้ให้ เพื่อใช้สำหรับการสุ่มโดยเฉพาะ) ซึ่งอาจจะไม่สามารถการันตีได้เสียทีเดียวว่าเป็น True random จริงจาก Source หรือไม่ รวมถึงการจัดการหลัง Seed เองก็ใช้เทคนิคของ Pseudorandom ผสมด้วย จึงขอเรียกว่า Secure Pseudorandom ดีกว่า (แต่ในเชิง Technical ก็ถือว่า Secure มากพอที่จะเอามาทำเรื่องของ Cryptography ได้แล้วนะ)
ขอยกตัวอย่างจาก 3 programming language ที่ผมคุ้นเคย
ภาษา Python
- Pseudorandom: ใช้ Mersenne Twister เป็น algorithm ที่ใช้อยู่ใน random module
- Secure Pseudorandom: อยู่ในsecrets module สำหรับการทำ Cryptography (ใช้ os.urandom() เป็น Entropy source)
ภาษา Java
- Pseudorandom: ใช้ XORShift / Linear congruential generator (หรือ ตามมาตรฐาน Browser) เป็น algorithm ของคำสั่ง Math.random()
- Secure Pseudorandom (on browser): Web Cryptography API (คำสั่งwindow.crypto.getRandomValues() ) (Entropy source ขึ้นอยู่กับ javascript engine ของ browser เลย แต่พื้นฐาน algorithm คือ cryptographically secure random number generator — CSPRNG)
- Secure Pseudorandom (on Backend nodejs): อยู่ใน crypto module สำหรับการทำ Cryptography (Entropy source ขึ้นอยู่กับสิ่งที่ build-in ใน OS เช่น จาก /dev/urandom, /dev/random ใน Unix / Macos หรือจาก CryptoAPI ใน Windows)
ภาษา Go
- Pseudorandom: ใช้ Mersenne Twister เป็น algorithm ของmath/rand package
- Secure Pseudorandom: อยู่ในcrypto/rand package สำหรับทำ Cryptography (Entropy source ขึ้นอยู่กับสิ่งที่ build-in ใน OS เช่น จาก /dev/urandom, /dev/random ใน Unix / MacOS หรือจาก CryptoAPI ใน Windows)
ดังนั้น use case ไหนควรใช้ random แบบไหนเองก็ต้องเลือกใช้ให้เหมาะสมกับโจทย์ด้วยเช่นกัน
เราได้อะไรจากการรู้เรื่องนี้บ้าง
สิ่งที่ผมได้เรียนรู้คือ “การสุ่มเป็นโจทย์ที่อาร์ตมาก” แต่ก็เป็นโจทย์ที่สามารถทำได้ หากเราสามารถ scope โจทย์ลงมาให้ดีพอสำหรับทำเรื่องนี้ ในท้ายที่สุดเราก็อาจจะตอบไม่ได้หรอกว่าคอมพิวเตอร์มันสุ่มเหมือนมนุษย์แล้วจริงๆหรือป่าว เพราะเอาเข้าจริงๆ พวกเราเองก็อธิบาย “การสุ่มที่แท้จริง” ของตัวเราไม่ได้เหมือนกัน
ดังนั้นสิ่งที่เราต้องตั้งโจทย์เสมอคือ “เราจะเอาการสุ่มนี้ไปทำอะไรกัน” เพราะในท้ายที่สุด การสุ่มนั้นจะดีหรือไม่ ขึ้นอยู่กับว่าเรา “สุ่มไปเพื่ออะไร” เหมือนกันนะ
Reference
- https://review.thaiware.com/1863.html
- https://tashian.com/articles/a-brief-history-of-random-numbers/
- https://en.wikipedia.org/wiki/Middle-square_method
- https://en.wikipedia.org/wiki/Linear_congruential_generator
- https://en.wikipedia.org/wiki/Hardware_random_number_generator
ต้นฉบับ
ทำการย้ายมาจากบทความนี้ เนื่องจากต้องการรวมบทความที่เดียวกันไว้
